Bedienung der Grafiken¶
Viele Grafiken bieten eine Auswahlmöglichkeit mit der mehrere sogenannte "Features" gleichzeitig ausgewählt werden können.
Um zusätzliche Features in den Grafiken darzustellen, können man diese mit Strg + Linksklick auswählen.
Innerhalb der Grafiken werden die Messwerte der Punktes angezeigt, auf dem sich der Cursor befindet. Sie können mit Halten der linken Maustaste einen rechteckigen Ausschnitt ziehen, in den gezoomt werden soll. Um die Auswahl zurückzusetzen, finden Sie rechts oben eine Leiste mit Icons. Klicken Sie einfach auf das Icon mit dem Haus, dann wird die Grafik auf Ihren Ursprungszustand zurückgesetzt.
Projektbeschreibung¶
Dieser Demonstrator ermöglicht den Ablauf eines Maschine Learning Projekts des Digital Laboratory mit interaktiven Komponenten nachzuvollziehen. Der Use-Case war die Entwicklung eines ML-Modells, das anhand der Maschinen- und Prozessdaten vorhersagen soll, ob der Durchmesser einer Bohrung sich innerhalb der Toleranz befindet.
Mit einer 5-Achs-Fräsmaschine wurden mehrere hundert Bohrungen in C45E gefertigt und gleichzeitig Maschinen- und Prozessdaten aufgezeichnet. Der konkrete Prozessablauf ist im nachfolgenden Video beschrieben. Die Istmaße der Bohrungen wurden mit dem Messmittel der Maschine ermittelt. Bohrungen, die innerhalb der Toleranz liegen sind mit Label 0 markiert, diejenigen außerhalb haben das Label 1.
Die Maschinen-/Prozessdaten werden in einer Datenbank gespeichert. Über ETL-Prozesse werden diese Daten in ein Data-Warehouse übertragen, um diese für die anschließende Verarbeitung besser zugänglich zu machen.
Abschließend werden unterschiedliche ML-Modelle mit den Daten trainiert und deren Vorhersagequalität bewertet.
Informationen zum Datensatz:¶
Dieser Datensatz enthält die Daten für die geriebenen Bohrungen. Jeder Reibvorgang (einer pro Bohrung) enthält Werte von 25 Sensoren. Insgesamt wurden über 1.300 Reibvorgänge durchgeführt. Im folgenden wird oft von "Datenpunkten" gesprochen; ein Datenpunkt stellt einen Reibvorgang mit den zugehörigen Sensormesswerten dar. Für Analysen ist dies ein vergleichsweise kleiner Datensatz, aber dennoch ausreichend, um die grundlegenden Konzepte und Herausforderungen zu verdeutlichen.
An dieser Stelle lohnt es sich den Datensatz einmal genauer anzusehen. Dazu gibt es eine Tabelle, welche alle Sensoren des Datensatz auflistet.
| Energy Savings Spindelleistung [W] | Energy Savings Achsleistung Z [W] | Spindel Position MCS [Grad] | Spindel rel. Leistung [%] | Spindeldrehzahl [RPM] | Spindel MPC Peak [%] | Spindel MPC Veff Total [mm/s] | Temperatur Spindel [°C] | TCC Axialkraft Zug [kN] | TCC Biegemoment [Nm] | TCC Unwucht [%] | X1 Achse rel. Leistung [%] | Y1 Achse rel. Leistung [%] | Y1 Achse Temperatur Schlitten [°C] | Z1 Achse Vorschub [mm/min] | Z1 Achse Position MCS [mm] | Z1 Achse rel. Leistung [%] | Zeitstempel | Energy Savings Achsleistung X [W] | TCC Axialkraft Druck [kN] | X1 Achse Vorschub [mm/min] | X1 Achse Position MCS [mm] | A1 Achse rel. Leistung [%] | Label | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.126359 | 53.527900 | 179.816218 | 0.500000 | 317.379310 | 1.000000 | 0.500000 | 28.105000 | 1.258537 | 2.500000 | 0.183158 | 1.500000 | 0.500000 | 24.765000 | 354.875000 | -304.447544 | 13.739130 | 2019-11-20 09:34:30.170 | 416.8530 | 0.052632 | 1011.666667 | 367.5250 | 5.500000 | 0 |
| 1 | 1.763218 | -223.576625 | 184.350446 | 0.507463 | 317.500000 | 0.666667 | 0.500000 | 28.067143 | 0.674074 | 0.850000 | 0.189630 | 4.166667 | 0.500000 | 24.766667 | 8.800000 | -302.581802 | 13.766667 | 2019-11-20 09:34:53.847 | 416.8530 | 0.052632 | 1011.666667 | 367.5250 | 5.500000 | 0 |
| 2 | 1.398177 | 382.341625 | 181.430268 | 0.500000 | 317.300000 | 2.333333 | 0.500000 | 28.067143 | 0.047826 | 0.478261 | 0.142264 | 9.000000 | 0.600000 | 24.800000 | -156.000000 | -302.535946 | 12.562500 | 2019-11-20 09:35:16.250 | -60.9040 | 0.048148 | 3049.500000 | 384.0300 | 5.500000 | 0 |
| 3 | 1.065278 | 700.204571 | 177.692973 | 0.492308 | 317.128205 | 1.666667 | 1.000000 | 28.032857 | 0.050000 | 0.500000 | 0.151346 | 0.500000 | 1.000000 | 24.800000 | 26.000000 | -303.418349 | 17.350000 | 2019-11-20 09:35:38.677 | -111.6570 | 0.054286 | 0.000000 | 397.9600 | 5.500000 | 0 |
| 4 | 0.225588 | -132.687143 | 175.616696 | 0.508475 | 317.062500 | 1.500000 | 1.000000 | 28.000000 | 0.050000 | 0.529412 | 0.141404 | 3.000000 | 0.666667 | 24.800000 | 67.909091 | -302.540270 | 16.608696 | 2019-11-20 09:36:00.879 | 4.0605 | 0.052000 | 4358.500000 | 410.0850 | 5.500000 | 0 |
| 5 | 0.213056 | 127.758000 | 183.630089 | 0.493151 | 317.393939 | 1.666667 | 1.000000 | 27.970000 | 0.050000 | 0.470588 | 0.143654 | 11.750000 | 0.800000 | 24.800000 | -129.636364 | -302.599820 | 13.850000 | 2019-11-20 09:36:23.300 | 36.5425 | 0.050000 | 1133.000000 | 428.0700 | 5.500000 | 0 |
| 6 | 0.201842 | 930.675571 | 178.612072 | 0.500000 | 317.250000 | 1.500000 | 0.666667 | 27.936000 | 0.050000 | 0.500000 | 0.134583 | 1.500000 | 1.000000 | 24.800000 | -92.363636 | -303.499636 | 15.312500 | 2019-11-20 09:36:45.710 | -203.0130 | 0.064286 | 0.000000 | 442.9600 | 5.533333 | 0 |
| 7 | 0.210714 | 322.866222 | 179.166518 | 0.500000 | 317.139535 | 2.000000 | 0.428571 | 27.902000 | 0.050000 | 0.520000 | 0.194231 | 2.857143 | 0.800000 | 24.800870 | 77.884615 | -303.518182 | 19.062500 | 2019-11-20 09:37:07.911 | 415.4995 | 0.059091 | 4252.000000 | 453.0250 | 5.454545 | 0 |
| 8 | 0.798958 | -269.504125 | 182.774375 | 0.500000 | 317.111111 | 1.333333 | 0.500000 | 27.864615 | 0.050000 | 0.485714 | 0.158750 | 2.333333 | 0.666667 | 24.800000 | 25.166667 | -302.617027 | 15.666667 | 2019-11-20 09:37:30.317 | 415.4995 | 0.045455 | 2775.000000 | 471.8750 | 5.500000 | 0 |
| 9 | 0.824731 | 85.094500 | 187.007257 | 0.507463 | 317.105263 | 1.500000 | 1.000000 | 27.842000 | 0.033333 | 0.500000 | 0.181852 | 18.250000 | 1.857143 | 24.837143 | -91.636364 | -302.614775 | 13.526316 | 2019-11-20 09:37:52.718 | 1607.4100 | 0.080000 | -8254.000000 | 369.9875 | 5.333333 | 0 |
Erklärung¶
Jede Zeile entspricht einem vollständigen Reibvorgang, jede Spalte einer aufgenommenen Messgröße mit der entsprechenden Einheit in eckigen Klammern. Die verwendeten Sensoren überwachen die Wirkleistung, Temperatur und Position der Achsen und der Spindel, sowie Prozesskräfte, wie Biegemomente, Axialkräfte und Unwucht.
Da für jeden Reibvorgang nur ein repräsantativer Wert pro Messgröße notwendig ist, aber über die Prozessdauer sehr viele Messwerte gespeichert werden, wird hier deren arithmetische Mittelwert verwendet.
Erforschen einzelner Variablen mit Hilfe von Graphen¶
Der erste Schritt ist die visuelle Datenanalyse. Durch Darstellung der Daten in unterschiedlichen Diagrammen können Muster sichtbar gemacht werden, beispielsweise Korrelationen zwischen Variablen oder vorhandene Ausreißer. Bei der Analyse einzelner Variablen ist vor allem die Verteilung der Messwerte einer Messgröße kann von Interesse sein. Einige Diagramme, die einzelne Messgrößen visualisieren, werden nachfolgend dargestellt.
Histogramm¶
Das Histogramm teilt die Daten in eine diskrete Anzahl an Klassen und stellt jede Klasse mit einem Balken dar. Dabei entspricht die Höhe der absoluten Anzahl der Messwerte in dieser Klasse. Somit wird die Verteilung der Messwerte einer Messgröße grob dargestellt. Mittels Histogrammen können Maxima und Minima schnell identifiziert werden. Außerdem kann eine grobe Gesamtverteilung schnell ermittelt werden. Histogramme sind oft ein guter Einstieg für Analysen, um einen Überblick über die vorhandenen Daten zu erhalten.
Violinengraph¶
Der Violinengraph zeigt im Vergleich zum Histogramm eine stetige Schätzung der Verteilung, zusammen mit einem Box-Plot, der markante Punkte der Verteilung darstellt. Die Verteilung des Violinenplots erfolgt dabei duch Kerndichteschätzung. Der Box-Plot zeigt den Median sowie die verschiedenen Quartile und Punkte welche außerhalb liegen (= Ausreißer).
Punktegraph (Scatterplot)¶
Scatterplots sind eine einfache Methode, um einen schnellen Überblick über statistische Zusammenhänge und Trends zu erkennen. Hier ist als X-Achse der zeitliche Verlauf verwendet worden. Im Gegensatz so Histogramm oder Violinengraph bietet sich also hier die Möglichkeit zeitliche Veränderungen einer Variablen zu untersuchen. MIt Scatterplots können auch zwei Variablen mit einander in Beziehung gesetzt werden, mehr dazu in Abschnitt ...
Dichteverteilung mit Violinengraph¶
Dieser Graph zeigt die Verteilung in Form eines Violinenplots oder Boxplots über dem entsprechenden Histogramm dar. Hier lässt sich der Zusammenhang von Violinenplot und Histogramm erkennen. Die Kombination von einzelnen Diagrammen bietet nicht zwangsweise einen Mehrwert, bietet aber den Vorteil einer gemeinsamen Darstellung mehrerer Diagramme in einer Grafik.
Beispiel:¶
Vergleicht man die Visualisierung der Variable Spindeldrehzahl und Spindel Position MCS sind Unterschiede gut zu sehen. Die Drehzahl folgt am nahezu einer Normalverteilung, wie sich an Histogramm und Violinenplot erkennen lässt. Außerdem sind keine zeitlichen Verläufe im Scatterplot zu erkennen.
Die Drehzahl dagegen ist ein extremer Fall eine multimodalen Verteilung: es kommen fast aussließlich drei Werte vor. Der Violinenplot glättet dabei die Verteilung zwischen den Modi, obwohl in diesen Wertebereichen teilweise gar keine Messwerte vorliegen. Der Scatterplot zeigt außerdem den zeitlichen Ablauf einzelner Phasen mit unterschiedlichen Drehzahlen.
Erforschen der Zusammenhänge zwischen mehreren Variablen¶
Punktegraph (Scatterplot)¶
Mit einem Scatterplot kann eine als unabhängig angenommene Variable auf einer Achse dargestellt werden und eine als abhängig angenommene Variable auf der anderen Achse. Wird anhand der Position der Datenpunkte ein Muster erkennbar, liegt eine Korrelation vor. Die Graphen links oben und rechts unten (auf der Hauptdiagonale) im nachfolgenden Diagramm zeigen eine ideale lineare Korrelation, da beide Achsen dieselbe Variable abbilden. Die übrigen Graphen sind immer eine Kombination aus den gewählten Messgrößen.
Beispiel:¶
Vergleicht man Energy Savings Spindelleistung [W] mit Spindel rel. Leistung [%] sihet man eine deutliche lineare Korrelation bei höheren Bereichen, allerdings nicht so stark, wie man es erwarten würde. Wählt man zusätzlich Energy Savings Achsleistung Z [W] aus, zeigen diese Variable keinen Zusammenhang mit den anderen.
Außer linearen Korrelation können auch andere Zusammenhänge deutlich werden. Wählt man beispielsweise X1 Achse Vorschub [mm/min] und X1 Achse Position MCS [mm] aus, ergibt sich ein zyklisches Muster und keine lineare Korrelation.
Korrelationsmatrizen¶
Lineare Korrelationen können mittels Pearson-Korrelationskoeffizienten auch über eine Metrik quantifiziert werden. Der Wert reicht von -1 bei maximaler negativer Korrelation bis +1 bei maximaler positiver Korrelation. Werte gegen 0 zeigen, dass keine lineare Korrelation vorliegt.
Die Darstellung der Korrelationskoeffizienten erfolgt häufig in einer Heat-Map und das Ergebnis ist eine Korrelationsmatrix. Über Farbe kann dabei visuell schnell die Korrelation bewertet werden. Besonders interessant ist dabei die Korrelation mit dem Zielzustand (=Label), da diese Aufschluss darüber gibt, welche Messgrößen das Prozessergebnis beeinflussen.
Beispiel:¶
Wählt man Label, Spindeldrehzahl [RPM] und Y1 Achse rel. Leistung [%] werden die Unterschiede deutlich. Zwischen der Y-Achsen-Leistung und den übrigen Werten besteht keine Korrelation, allerdings korreliert die Spindeldrehzahl mit unserem Label mit einem Koeffizienten von 0,59.
Pair Plot¶
Beim paarweisen Vergleich zweier Variablen lassen sich Scatterplots und Verteilungsgraphen in einem sog. Pair Plot kombinieren. Dabei erfolgt eine Unterscheidung der beiden Klassen niO/iO, so dass nach Variablenkombinationen gesucht werden können, die eine Trennung der beiden Klassen ermöglichen.
Beispiel:¶
Stellt man die Verteilung der einzelnen Klassen über die Variable Energy Savings Achsleistung Z [W] dar, überlappen sich beide Verteilungen großflächig. Eine Trennung der Klassen über ausschließlich diese Variable ist also nicht möglich.
Machine Learning¶
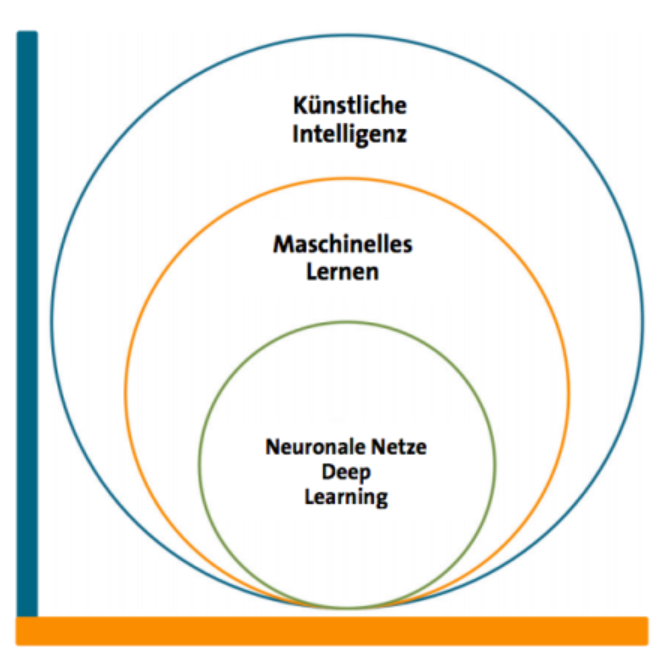
Machine Learning ist ein Teilbereich der Künstlichen Intelligenz, der es einem System ermöglicht, mithilfe lernender Algorithmen Zusammenhänge in Daten zu erkennen. Diese Zusammenhänge bezeichnet man aufgrund der gleichförmigen Struktur als Muster.
Damit die Algorithmen erfolgreich Muster erkennen können, wird eine repräsentative Stichprobe des Anwendungsgebiets benötigt. Nachdem diese ermittelt und validiert wurde, werden Merkmale gewählt. Da bei mehr als drei Merkmalen eine direkte Visualisierung nicht mehr möglich ist, ist das Finden von Mustern eine komplexe Aufgabe. Außerdem können manche Merkmale entfernt werden, falls sie keine wichtigen Informationen zur Klassifikation beisteuern. Anhand der Datenstrukturen und Eigenschaften kann nun ein Modell gewählt werden. Dabei unterscheidet man zwischen Klassifikatoren und Regressoren.
Multiple und Logistische Regression¶
Was ist Regression?¶
Bei linearer Regression sucht man nach Beziehungen zwischen einer abhängigen Zielgröße $y$ und den zugehörigen Einflussgrößen, den unabhängigen Variablen $\textbf x$, wobei die Einflussgrößen $\textbf x$ und die Zielgröße $y$ kontinuierliche Werte annehmen.
Im 2-dimensionalen Fall bedeutet das, eine Gerade der Form $y = a + b x$ zu finden, die die realen Daten am besten beschreibt. Wie gut die Regressionsgerade die Daten beschreibt, wir über einen Fehler (Abstand der Datenpunkte zur Geraden) quantifiziert. Meist wird hier der Mean-Squared-Error verwendet:
$MSE = \frac{\sum^n_{i=1}{(y_i - y_i^p)}^2}{n} $
Lineare Regression kann auch in mehr Dimensionen stattfinden, je nach Anzahl der unabhängigen Variablen erweitert sich die Gleichung zu:
$y = a + b_1x_1 + b_2x_2 + b_3x_3 \ldots $
In 3 Dimensionen entspricht das geometrisch einer Ebene durch den Merkmalsraum und ein höheren Dimensionen einer sogenannten Hyperebene.
Logistische Regression¶
Lineare Regression ist für die Vorhersage kontinuierlicher Werte geeignet, allerdings nicht für Klassifikation. In diesem Use-Case beschreibt die Zielvariable $y$ die beiden Klassen niO/iO und diese werden mit 1 und 0 beschrieben.
Allerdings werden diese Werte bei logistischer Regression nicht als Klassen interpretiert, sondern als Zahlen. Des Weiteren wären bei einem linearen Regressionsmodell als Vorhersage Werte im Bereich $(- \infty, + \infty)$ möglich, was die Vergleichbarkeit einzelner Vorhersagen erschwert, da es keine sinnvolle Abgrenzung der Klassen gibt.
Daher wird bei Klassifikation die sog. Logistische Regression verwendet. Diese liefert nur Vorhersagen im Bereich $(0, 1)$, die dann als Wahrscheinlichkeiten für die Zugehörigkeit zur entsprechenden Klasse interpretiert werden können.
Die Logistische Regression verwendet genauso wie Lineare Regression die Kombination der unabhängigen Variablen:
$y = a + b_1x_1 + b_2x_2 + b_3x_3 \ldots $
allerding werden diese dann als Eingabe für die Logistische Funktion verwendet:
$\text{f}(y)=\frac{1}{1+exp(-y)}$.
Der Funktionswert f(t) entspricht dann der Wahrscheinlichkeit $P(Klasse=1)$.
Der Graph mit den bekannten Datenpunkten verfolgt eine S-Kurve mit großer Steigungsänderung in der Mitte:
Entscheidungsbäume¶
Entscheidungsbäume bestehen aus "Blättern", "Knoten" und "Kanten". Dabei entspricht ein Blatt genau einer Klasse, jeder Knoten entspricht einem Test von einem oder mehreren Klassenattributen und eine Kante ist ein mögliches Testergebnis. Entscheidungsbäume betehen aus sogenannten Merkmalen, welche diskrete Eigenschaften besitzen. Das beudetet, dass die Merkmale abzählbar sind und nicht unendlich viele Werte annehmen können.
Muster mit diskreten Merkmalen können nicht numerisch klassifiziert werden, da
- Merkmale meist keine natürliche Ordnung besitzen (z.B. Farben)
- aus Ähnlichkeiten von Werten nicht auf dieselbe Klasse geschlossen werden kann
Ziel eines Entscheidungsbaumes ist das Finden des besten Attributs. Dabei ist das beste Attribut dasjenige, welches die Beispiele am besten aufteilt $\rightarrow$ kurze Pfade mit kleinen Bäumen.
Großer Vorteil von Entscheidungsbäumen ist das einfache Verständnis des Ergebnisses. Fast jeder hat schon Entscheidungsbäume in der ein oder anderen Form gesehen. So können Ergebnisse schnell nachvollzogen werden.
Entscheidungsbäume spiegeln durch Ihre "Tiefe" auch Ihre Komplexität wider.
Vorteile:
- Entscheidungsbäume können von Natur aus eine Mehrklassenklassifizierung durchführen.
- Sie bieten die meiste Modellinterpretierbarkeit, da es sich hierbei lediglich um eine Reihe von if-else-Bedingungen handelt.
- Sie können sowohl numerische als auch kategorische Daten verarbeiten.
- Nichtlineare Beziehungen zwischen Merkmalen haben keinen Einfluss auf die Performance der Entscheidungsbäume.
Nachteile:
- Eine kleine Änderung im Datensatz kann die Baumstruktur instabil machen, was zu Abweichungen führen kann.
- Wenn Klassen unausgewogen sind, werden underfit-trees erstellt $\rightarrow$ Datensatz vor Anpassung an Entscheidungsbaum abgleichen!
Support Vector Machines¶
Ein generelles Problem bei der Klassifizerung ist die Generalisierungsfähigkeit, also die Fähigkeit unbekannte Daten richtig zuzuordnen. Man kann nun für die Daten die einzelnen Klassen als Punkte im Raum visualisieren (natürlich nur 2 & 3-Dimensional möglich). Diese Klassen trennt man durch sogenannte Trennebenen. Das Ziel ist es, die Trennebene mit einem maximalen Abstand zu allen Klassen im hyperdimensionalen Raum zu legen. Deshalb werden SVMs auch oft als " Maximum Margin Classifier " bezeichnet.
Ein großes Problem stellt allerdings die Trennung von Hyperebenen im höherdimensionalem Raum dar. Man muss dazu die einzelnen Merkmale (Klassen) in einen höherdimensionalen Raum transformieren um diese dort trennen zu können. Dazu nutzt man verschiedene " Kernel "-Funktionen; diese beschreiben den Transformationsprozess von niedrigen in hochdimensionale Räume. Es gibt viele verschiedene Kernel-Funktionen, diese müssen immer je nach Problem neu ermittelt und angepasst werden.
Hier ist im Beispiel ist eine einfache Trennebene, die zwei Klassen im 2-Dimensionalen Raum voneinander trennt, zu sehen. Die durchgezogene Linie ist dabei der maximale Abstand zwischen den beiden Klassen.
Vorteile:
- Effektiv in hochdimensionalen Räumen.
- Auch für Probleme geeignet, in welchen die Anzahl der Dimensionen größer ist als die Anzahl der Beispiele.
- Speichereffizient, da ein Subset der Trainingspunkte erzeugt wird.
- Sehr flexibel, da verschiedene Kernelfunktionen für die Klassifikationsfunktion verwendet werden können.
Nachteile:
- Wenn die Anzahl der Features viel Größer als die Anzahl der Beispiele ist, passt der Algorithmus sich an das Problem an $\rightarrow$ Overfitting.
- SVMs geben keine direkte Wahrscheinlichkeit zurück, sondern müssen kostenintensiv in einen höherdimensionalen Raum transformiert werden.